Introduction

Comme je le répète 15 fois par jour depuis 5 ans, je tente de rafraîchir mon blog en lui offrant une nouvelle peau qui en réalité tient davantage d'une peau de banane trop mûre remplie d'oeufs de drosophiles que d'une peau de jeune phoque qui vient de prendre une douche.

J'avais choisi une technologie et réussi à me convaincre de me lancer tout de suite et pas attendre la prochaine version et voilà que, dans un état de flow absolu, je tombe sur l'endroit où je voulais estimer le temps de lecture de mes articles.

Et c'est là que tout à basculé.

Comment qu'on estime le temps de lecture?

Facile. Il suffit de dégotter la moyenne de mots par minute que peuvent lire les gens moyens en moyenne et on divise le nombre de mots du texte évalué par cette valeur, et BOOM on a des minutes.

Reste plus qu'à trouver combien de mots ont échoué dans un de mes articles pour calculer un temps de lecture tellement décourageant que c'est vraiment pas une bonne idée d'en parler avant même que ma poignée de un ou deux valeureux lecteurs ne commencent leur lecture.

Cependant, nous voilà bien embêtés parce que l'ORDINATEUR n'a aucune idée de ce que c'est un mot.

Vous vous souvenez de votre oncle quand il disait "Tu sais Timmy, l'ordinateur il comprends uniquement le binaire et rien d'autre" — He ben il avait raison votre oncle bizarre.

Les ordinateurs encodent le texte en binaire caractère par caractère.

C'est-à-dire qu'une lettre, un élément de ponctuation et même un espace correspondent tous à une certaine série de chiffres binaires.

Quelqu'un a dû un jour décider de quelle combinaison correspond à quel caractère, et le reste de la planète a dû accepter d'adopter ce système ou utiliser un autre. Il existe par conséquent plusieurs de ces conventions qui se sont aussi complexifiées avec le temps.

Au départ, c'était facile: une séquence de 8 bits correspondait à un caractère américano-centriste.

Je veux dire par là qu'ils ont d'abord codé les lettres utilisées en anglais et quelques éléments utiles à dessiner des interfaces console rudimentaires puisque, à l'époque, tout le monde utilisait un terminal en mode texte.

Aujourd'hui plus personne n'aurait l'idée saugrenue d'utiliser exclusivement un éditeur de texte qui fonctionne uniquement dans un terminal (c'est une blague on est relativement nombreux à faire ça, principalement pour épater les filles).

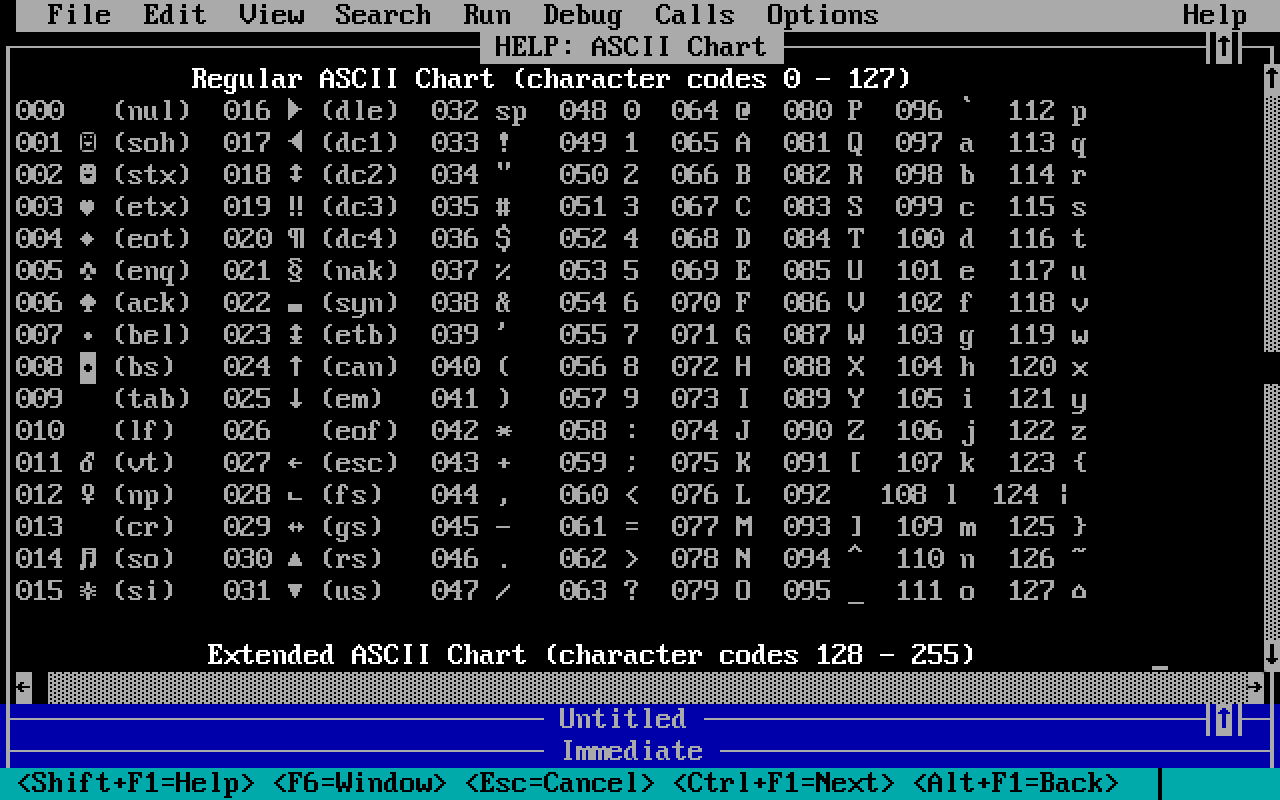
Les caractères non-latins étaient totalement absents alors que d'autres specimens extrèmement courants en Français (le "é" par exemple) se trouvent très loin derrière dans la table d'encodage.

Le texte est stocké tel une chaine de ces groupes de chiffres binaires (lesquels correspondent à des caractères, je rappelle) d'où l'appellation chaine de caractères en Français, dit aussi "string" en anglais (ce qui signifie "corde" ou "ficelle" et pas chaine, mais c'est pas grave).

Ces représentations de texte se retrouvent un moment ou l'autre en mémoire.

La mémoire étant une suite de groupes de chiffres binaires continus, les programmes doivent savoir où commencent et où se terminent les chaines de caractères en mémoire.

Cette info consiste généralement en un emplacement de départ et une longueur qui est traditionnellement en bytes (ou octet = 8 bits). Mais pas obligatoirement, ça dépend de comment on choisit d'encoder le texte en binaire.

Par exemple, ce bon vieux JavaScript qui nous occupe dans le cadre de ma courante problématique utilise un groupe de deux bytes comme unité de longueur.

Je vais d'ailleurs totalement zapper cette affaire et me fourvoyer initialement dans mes calculs.

OK, d'accord. Pourquoi j'explique tout ça? C'est juste gratuit?

Non! Le but était de bien souligner que le nombre de mots d'un texte est d'office inconnu mais que l'on dispose immédiatement d'une mesure de longueur (qui vaut ce qu'elle veut) sans aucun traitement nécessaire parce que le processeur doit absolument connaître cette valeur pour récupérer ce qu'il faut en mémoire.

Bien évidemment, cette "longueur" contient aussi toute la ponctuation, les espaces, retours à la ligne et les nombreux emojis que j'utilise 🦆🩲 et qui comptent d'ailleurs pour plusieurs caractères.

Mais alors, comment trouver le nombre de mots?

Normalement pas à partir de la longueur en bits ou groups de bits du text, c'est les gens louches qui font ça.

Les gens normaux utilisent une librairie qui s'occupe de la logique pour eux mais on tourne toujours autour de l'idée qu'un mot est séparé d'autres mots par des espaces ou autres caractères apparentés comme les retours à la ligne et tabulations.

Outre les différents caractères de "type espace" il y a aussi la possibilité que plusieurs de ces caractères se suivent, auquel cas il ne faut en compter qu'un seul.

De plus, le contenu de mes articles contient du HTML (à ne pas reproduire à la maison sans garde-fous pour des raisons de sécurité), en majeure partie constitué d'une quantité absurde de tabs <p>.

La plupart n'ont ceci dit pas d'effet sur le décompte d'espaces parce qu'ils sont toujours collés à un mot, et compte dès lors pour un mot, avec ce mot (??).

Quoi qu'il en soit et même s'il existe plusieurs techniques, compter les mots revient à parcourir tout le texte et regarder chaque caractère.

"Ben dis donc là DkVZ, compter chaque caractère de tes articles c'est une épreuve non?"

Ben pas vraiment. Il faut déjà parcourir tout le temps pour générer la table des matières avec un algorithme récursif que j'arrive plus à comprendre quand je le relis (cherche les "titres").

Ceci dit, parcourir même un très long texte en JavaScript c'est juste immédiat sur un ordi moderne.

Mais bon, vous me connaissez. Non vous me connaissez pas en fait. J'ai des problèmes.

J'ai des problèmes

Le fait que mon texte soit parcouru plusieurs fois et qu'une de ces fois soit mon algorithme infernal qui génère la table des matières ne gène. J'aime pas.

En soi, les animations de mon blog consomment probablement bien plus que les histoires de JavaScript appliqué au texte.

Est-on vraiment à un parcours de texte près, même sur un appareil un peu nul? Non. Quand t'es sur le WAP depuis ton 3310 t'es pas à 4 secondes près.

Imaginons que ça m'empêche tout de même de dormir la nuit, n'y a-t-il pas des solutions simples pour obtenir le total de mots de manière efficace?

Oui! Je pourrais pas exemple ajouter ce calcul au niveau du backend voire de sa base de données lors de modifications ou encore utiliser un bon vieux batch qui se lance de temps à autre.

Evidemment j'ai choisi de partir totalement ailleurs dans le projet qui doit désormais détenir mon record personnel de temps passé dessus par rapport à son utilité (qui tend vers 0 mais est tout de même un poil de tardigrade plus élevé).

Tout ça pour finalement cacher une partie de ces estimations de temps parce que, afficher "145 minutes de lecture lol" je pense que ça risque d'effrayer tout le monde y compris les bots.

Et si je pouvais estimer le nombre de mots à partir de la longueur du texte et par la même occasion essayer d'écrire des titres un peu plus courts si possible?

Ben ouais. Je vais me creuser ce trou et y poser ma tente Quechua.

Le postulat est plus simple que celui de la relativité générale: imaginons qu'il existe un rapport évident entre la longueur du texte et le nombre de mots que je pourrais utiliser pour estimer le nombre de mots à partir de la longueur et est-ce que je viens t-y pas de répéter le titre de cette section une fois de plus?

Quand le nombre de mots augmente, forcément la longueur augmente aussi. Cool. C'est toujours bon signe ça.

Je pourrais vaguement le vérifier en prenant la longueur moyenne des mots utilisés dans les textes en français pour en tirer un rapport foireux de MOT/LONGUEUR.

Multiplier ce facteur de MOT/LONGUEUR par une LONGUEUR ça me donne des MOTs.

D'après les internets et quelqu'un qui a probablement compté des mots pour de vrai à la main dans des textes, la longueur moyenne de mots utilisés en français serait quelque part entre 4,5 et 5.

Reste plus qu'à trouver un texte de test. J'avais pensé à la bible mais elle est divisée en versets précédés de leurs noms qui ajoutent du coup tout un tas de mots de la même longueur.

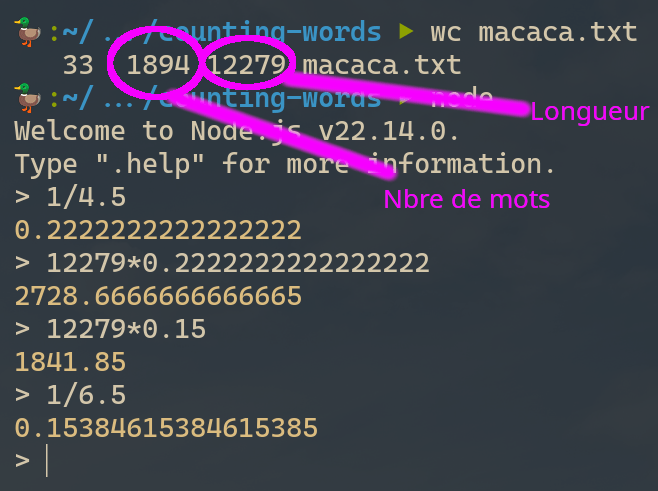
Prenons plutôt un extrait de l'article Wikipedia sur le Macaca Sylvanus (c'est un singe) que j'ai mis ici si vous souhaitez vérifier mes calculs.

Je vais utiliser la commande UNIX WC (signifie Word Count et pas TOILETTE) pour calculer la longueur et le nombre de mots.

Okay le nombre de mots que je prédis avec une longueur moyenne de 4,5 est beaucoup trop élevé par rapport à la réalité, je suis pas loin d'une erreur de 100%.

J'ai vraiment pas l'intention de le vérifier mais je me pense que le soucis vient de la ponctuation qui est comptée comme faisant partie des mots dans mon cas et pas dans le strict sens littéraire.

Puis y a aussi tous les espaces et connexes qui comptent dans la longueur du fichier mais pas dans la taille de mots au sens littéraire non plus.

La taille de mot moyenne dans ce cas serait plus proche de 6,5, qui correspond à un facteur mot/longueur d'environ 0,15. Retenons ce chiffre pour plus tard.

Où est mon vieux cours de stats

Bon ben écoutez, je vais récupérer tous mes articles et chercher un moyen de compter leur nombre de mots puis regarder si le rapport entre ce nombre et leur longueur est plus ou moins constant.

Décorons tout ça avec des moyennes et autres médianes et écarts types et ce sera tout bon.

Que vais-je utilise pour ces calculs?

Les programmes appelés communément "feuilles de calcul" possèdent toutes ces fonctions et classent naturellement les données en colonnes.

En informatique on a un vieux gag persistant qui dit qu'à peu près tous les problèmes au monde peuvent être résolus par Excel mais que peut-être parfois on devrait pas. Sauf cette fois-ci, là, pour une fois, il faudrait vraiment que j'utilise Excel.

Je vais pas utiliser Excel.

j'en ai même pas besoin, on peut même dessiner des graphiques en CSS sans Excel (sera important à retenir pour plus tard quand je vais quand même utiliser Excel):

Je ne vais pas non plus utiliser un langage spécialisé pour les stats. Ni même étendre le backend du blog qui a déjà toutes les fonctions d'accès DB, je vais plutôt démarrer un bon vieux projet en Go pour me calculer tout ça hors ligne à partir d'une copie de ma DB.

J'ai envie de m'essayer au multi-tâches en Go que je maîtrise très moyennement mais qui me semble convenir parfaitement à ce type de problèmes de prédiction et d'optimisation "à l'ancienne" (entendre: pas avec un vieux LLM et 6000€ de cartes graphiques).

Mon algorightme de comptage de mots consiste à coller quelques regex de l'enfer ensembles afin d'essayer de gérer tous les cas y compris la recherche de "&nbsp;" par exemple (qu'il faut transformer en espaces).

J'extrais aussi les légendes des images pour les compter dans le total alors. Je décide par contre d'exclure les extraits de code.

La plupart des tags HTML doivent être retirés totalement avec leur contenu (par exemple <svg>) alors que dans d'autres cas il faut bien garder le contenu, comme on le voit dans cette regex que j'utilise pour remplacement global par du vide.

var paReg = regexp.MustCompile(
	`</?(p|h\d|a|i|b|small|strike|sub|sup|abbr|span|blockquote|ul|ol|li|strong|em|del).*?>`,
)

Il ne faut pas oublier de retirer aussi les commentaires HTML, j'en laisse parfois trainer.

Finalement, pour calculer la longueur il s'agit de ne pas oublier de compter le nombre de "runes" UTF-16 puisque JavaScript utilise l'UTF-16 et pas l'UTF-8 comme Go et ma DB.

// Get the length of the string in UTF-16, which is what JS reports
// with the .length property.
func LengthUTF16(content *string) int {
	if content == nil {
		return 0
	}
	utf16Bytes := utf16.Encode([]rune(*content))
	return len(utf16Bytes)
}

Je me suis ensuite affairé à écrire tout un plan foireux d'exécution parallèle du comptage des mots qui répartit équitablement les articles à gérer sur autant de Goroutines qu'il n'y a de processeurs.

Je pense que ça sert à rien avec le nombre d'articles que j'ai mais l'exercice était sympa et il faut avouer qu'en terme de multi-tâche Go est vraiment bien foutu et je le préfère à C# même si on est pas à l'abri d'un bon vieux deadlock ou de bugs bizarres de channels qui ont été fermés ou pas.

Le projet est ici.

Démarche en deux parties qui aurait pu se faire en une partie avec Excel

Plutôt que d'avoir une feuille de calcul qui réagit en temps réel à mes manipulations je vais partir sur un utilitaire en ligne de commande (bien tiens) avec deux vieux modes:

• Calcul des longueurs, comptage de mots et affichage des statistiques pour tous les articles dans un ordre à déterminer
• Test des prédictions de différentes variables à décider pour un modèle à décider (ça fait beaucoup de trucs à décider)

Dans ma tête le modèle allait peut-être simplement consister à utiliser la valeur moyenne de mots par longueur de texte.

Cette grandeur va souvent revenir et se trouve en dessous de 1 (et au dessus de 0) parce que le mot moyen a une longueur toujours supérieure à 1 caractère et à plus forte raison dans mon cas puisque, comme évoqué précédemment, la ponctuation fait partie des mots dans mon modèle et la longueur des textes comprends pas mal d'autres éléments qui ne font pas partie des mots non plus mais gonflent tout de même cette longueur (contenu HTML, etc.).

J'imagine déjà qu'il faudra peut-être plusieurs facteurs différents de mots par longueur à appliquer pour différentes plages de longueur de texte (qui est la variable connue dans l'histoire, je rappelle).

Le principe reste de multiplier une longueur de texte par le bon facteur pour obtenir un nombre de mots qui se rapproche le plus possible de la réalité.

Le mode vérification devra mesurer la qualité de la prédiction à partir des distances entre les dites prédictions et la réalité.

Ne nous emportons pas trop (lol) là dedans et regardons d'abord s'il y a une relation qualitative entre la longueur de mes articles en UTF-16 et leur nombre de mots parce que sinon tout ça est encore plus inutile que prévu.

Voyons les stats à sortir:

• Longueur du contenu telle que JavaScript le donnerait avec la propriété .length
• Le décompte de mots qui correspond et fait sens pour le calcul du temps de lecture
• Le ratio de mots par longueur (je sais pas comment appeler cette chose, ce sera le ratio)

J'en profite pour ajouter les stats "classiques" principalement pour le ratio:

• La moyenne, je place beaucoup d'espoir dans la moyenne
• La médiane — un genre de mesure de "qualité" de la moyenne quoique pas nécessairement. Je l'utilise pas vraiment mais ça fait sérieux et cool de l'avoir dans le coin
• L'écart-type — Une mesure de la dispersion des valeurs, au plus bas elle est au mieux ce serait pour un modèle ultra simple de prédictions

L'écart-type se calcule en calculant la variance qui est la moyenne des carrés des écarts à la moyenne. Pourquoi les carrés? Ben je sais pas trop. En partie parce que ça rend le nombre d'office positif ce qui est important, mais la valeur absolue fait la même chose.

Il semblerait qu'il existe d'autres raisons mathématiques que je peux pas comprendre qui font que la variance entre dans le calcul d'autres choses avec des propriétés bien spécifiques et que si tu dé-carré la variance pour utiliser la valeur absolue à la place t'as toujours une mesure de l'écart à la moyenne mais elle fonctionne plus dans l'ensemble du génie statistique. Ou un truc du genre.

Puis cherche pas, on a toujours fait comme ça.

Note DEPUIS LE FUTUR: Mon calcul de la variance va souffrir de gros soucis d'approximations expliqués dans cette brève.

OK COOL. Sauf que maintenant ma mesure de dispersion c'est un truc au carré qui est pas très représentatif comme notion d'erreur parce que les carrés de valeur c'est beaucoup plus grand ou beaucoup plus petit.

D'où l'écart-type qui est simplement la racine carrée de la variance comme ça on dé-carré tout ce qu'on vient de carrer.

En gardant tous les articles je tombe sur ces valeurs:

Moyenne	Min	Max	Médiane	Déviation Std
0,120968	0,005051	0,156182	0,124370	0,024052

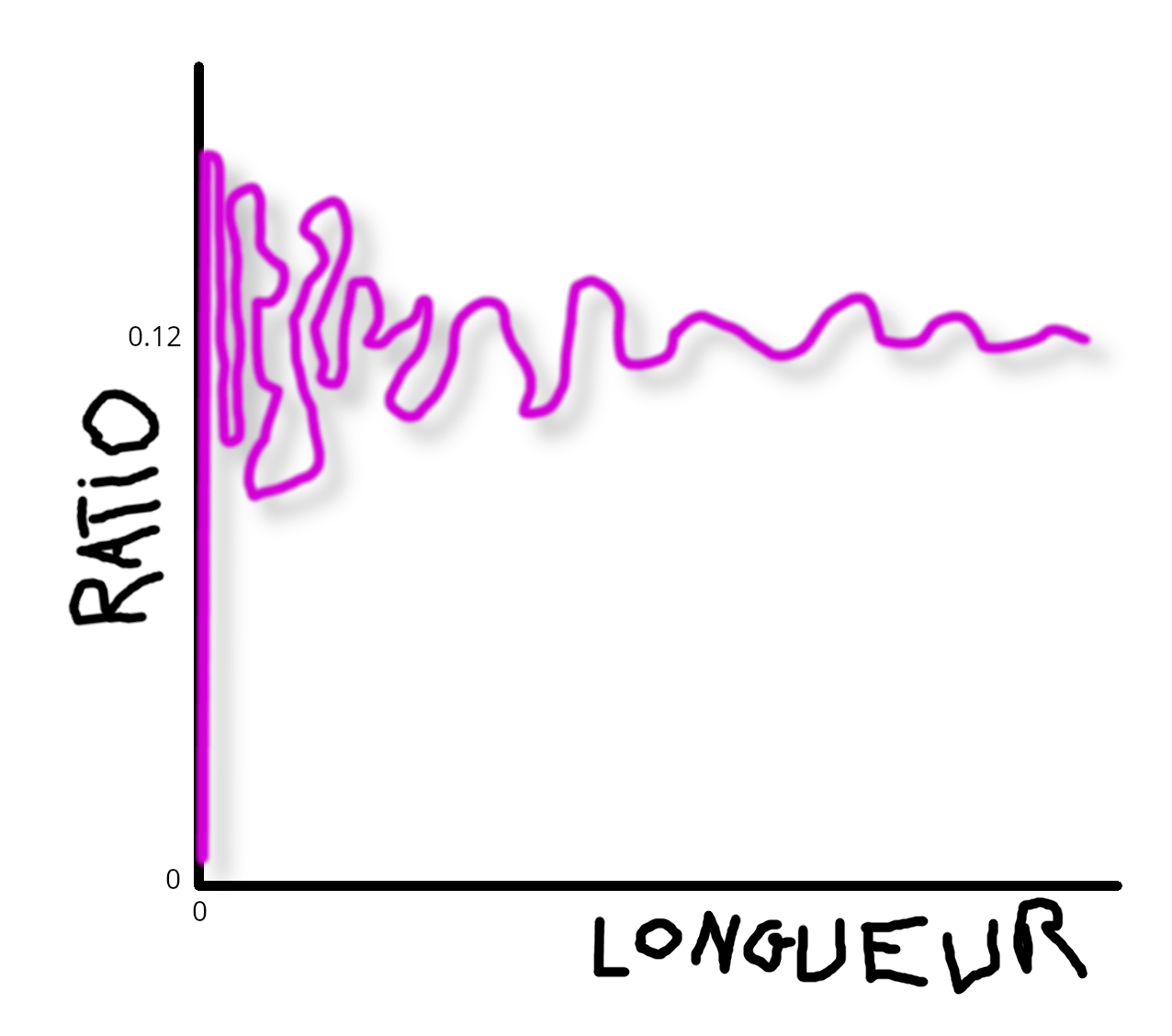
Le ratio a l'air de tourner autour de 0,12 avec un minimum visiblement très anormal à 0,005.

Dans la liste des articles je constate que celui-là n'a qu'un seul mot. Et... De fait. Il n'y a qu'un seul mot. C'est la vidéo présente dans la brève qui augmente considérablement la "longueur du texte" mais n'ajoute aucun mot au décompte.

Il faudra peut-être retirer certains de ces articles pour trouver un coefficient qui va bien, ce qui m'anènera à ajouter une bonne vieille option à mon programme pour ignorer certains articles ou brèves.

La déviation standard est toutefois relativement faible et nous ferait tourner autour de 0,10 et 0,15 (à la grosse louche n'est-ce pas).

Il se trouve que 0,15 c'est un ratio que j'avais calculé plus haut sur base d'un article Wikipedia. Mes mots sont sûrement moins châtiés que ceux de Wikipedia.

Je remarque soit dit en passant que le temps de lecture moyen de mes articles se trouve quelque part entre 10 et 11 minutes. Peut-être que la réputation de ce blog à avoir des articles beaucoup trop longs habite juste dans ma tête.

Me faut un graphique

Je pense qu'une petite représentation visuelle serait utile.

Encore un truc facile à sortir dans Excel. Oui on a compris maintenant.

La librairie go-echarts a l'air prometteuse. Je crois comprendre qu'elle est basée sur Apache ECharts qui a l'air très chouette aussi (librairie JavaScript).

Au début je pensais générer des images mais la librairie permet d'ouvrir un serveur qui présente une page avec un ou plusieurs graphiques et une très appréciable option de "zoom" dynamique qui pourrait être utile (en fait ce sera pas du tout utile).

Ma première intuition sera de grapher les ratios trouvés en fonction des longueurs de texte (sous forme de nuage de point) en espérant qu'ils trainent tous autour de la même horizontale.

Ce qui donne ceci:

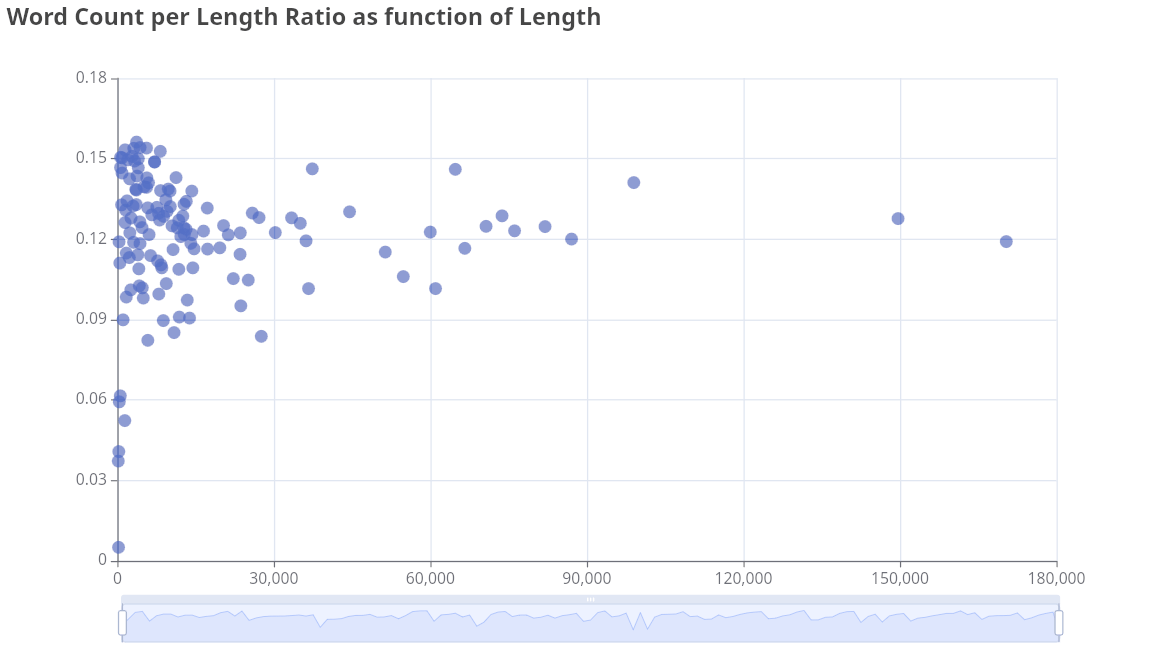
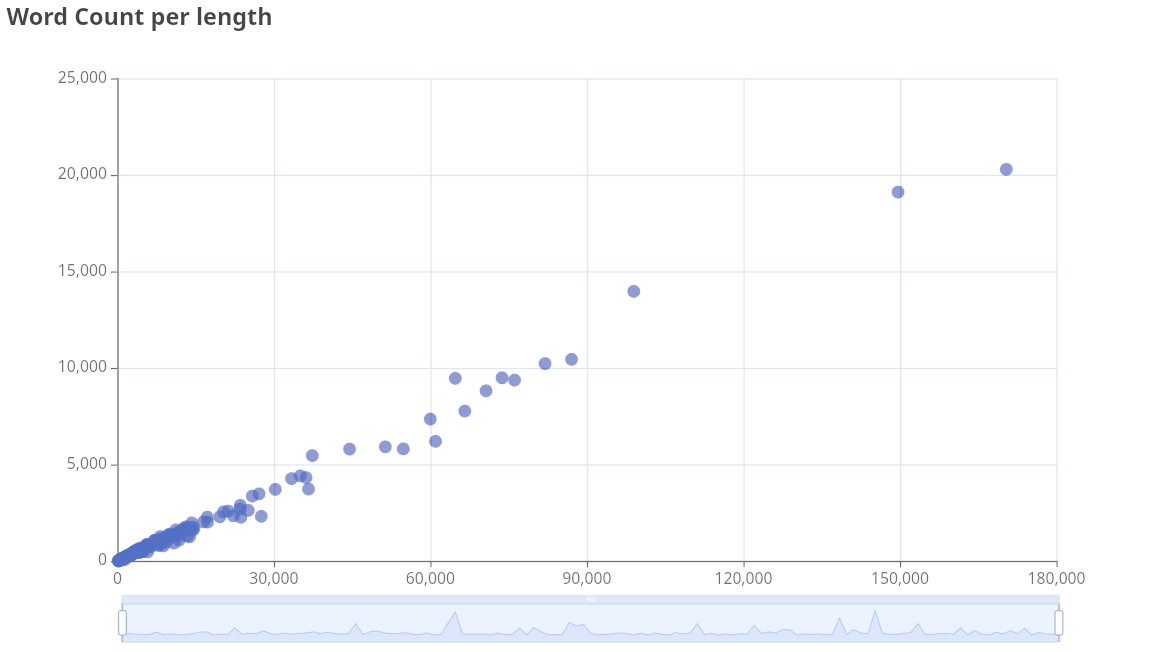
Je sais pas trop quoi en déduire à part que c'est pas ça qu'il fallait sortir comme graphique si c'est le ratio qui nous intéresse. Par hasard je tente de grapher le nombre de mots en fonction de la longueur de texte:

Attends une minute, ça me rappelle le labo physique et les régressions linéaires. Ce que je vois devant mes yeux ébahis n'est pas une hyperbole, ni un bol ni même la tête de Jésus apparaîssant sur un toast. Non, C'EST UNE DROITE.

En soi mon plan d'utiliser un mono-facteur pour prédire le nombre de mots créait une fonction y=rx où r serait le ratio, x la longueur du texte et y ce qu'on cherche à prédire — Il s'agit aussi d'une droite qui passe par le point 0,0.

En toute logique on est censés passer par l'origine parce qu'un texte de longueur 0 a d'office 0 mots dedans. Ceci dit si on calcule la régression linéaire à partir de ces données qui partent un peu en ribote dans les courtes longueurs, la meilleure droite ne passera pas par 0. Et on verra plus loin que le modèle fonctionne mieux comme ça.

Oui le modèle ne colle même pas à la réalité physique de l'univers mais il fonctionne quand même. J'ai aucune comparaison foireuse pour ce phénonème.

Essayons la régression linéaire

Dans la vraie vie il y a pas mal de choses qui sont plus ou moins linéaires. Et pas mal de choses qui ne le sont pas.

En gros on cherche une équation de droite, dont la forme complète est:

y = a + b*x

Comme je disais plus haut, on passe par l'origine si a vaut 0.

Enfin bon j'ai oublié le nom mathématique de ces termes. Le plan consiste à trouver la droite qui convient le mieux au nuage de point des données.

Cette droite minimise la distance par rapport aux points voisins et se trouve avec une formule magique impliquant les distances à la moyenne (au carré je crois, évidemment) et un bidule qu'on appelle la covariance mais on s'en balance parce que personne ne calcule les régressions linéaires à la main.

Non en fait voyez-vous, les gens utilisent Excel.

Et à voir la tête de la formule j'ai pas trop envie de programmer cet algorithme en Go ni d'importer une librairie infernale de stats.

Il ne reste plus qu'à se résoudre à s'asseoir sur sa fierté, exporter mes données et les important dans une feuille de calcul pour calculer la régression linéaire. Ouais. Tout ça pour ça. Je sais. Parfois la vie c'est nul et ça se termine dans Excel (enfin, LibreOffice CALC dans mon cas).

En pratique je peux juste copier coller une partie de la sortie de mon programme et pouf ça fait du CSV. Heureusement je ne dois rien ajouter dans le programme.

J'extrairai deux jeux de valeurs de régression linéaires (parce que LibreOffice me propose les deux calculs différents):

• Une qui est forcée de passer par l'origine
• Une qui ne l'est pas

Ces régressions n'ont pas la même valeur de b même si la première a évidemment a=0.

Vérification des prédictions

On va tester deux modèles indépendants:

• La régression linéaire
• Euh... Vaguement la régression linéaire aussi mais sans déviation d'abscisses et avec plusieurs coéfficients de régressions selon différentes plages de longueur de texte à déterminer

J'ai pas trop d'autres idées, je me vois pas vraiment dériver le bon ratio de ce genre de fonctions:

Pour tester les prédictions par régression linéaire j'utilise ce genre de ligne de commande hyper claire:

go run cmd/wordstats/main.go -mode verify -ignore-ids 79 -reg 0.123919042205186,-26.1899350298168

On calcule toutes les distances entre le nombre de mots prédits par le modèle et le vrai nombre de mots. Ce chiffre peut du coup être négatif jusqu'à ce que je décide de le mettre au carré. Puis de le racine carré. Non je vais pas faire semblant d'être mathématicien et laisser les carrés tranquilles.

Sortons aussi la déviation standard de la prédiction de nombre de mots — Générallement entre 330 et 350 pour les meilleurs "modèles" que j'ai testé.

Ce chiffre ne m'aide pas trop à juger la qualité des prédictions, et la distance non plus parce qu'une distance de 88 sur un article de 10000 mots c'est excellent alors que la même distance sur un article de 100 mots ça craint.

Va me falloir une autre métrique. Je pense diviser la distance par le véritable nombre de mots total histoire de montrer leur relation, qui devrait être toujours plus petite que 1.

J'ai des modèles ou c'est plus grand que 1 pour un ou deux articles — Ce qui signifie en gros que l'erreur de prédiction dépasse le nombre de mots (en d'autres mots: la prédiction est totalement à IECH).

Par contre cette valeur peut être négative quand la distance est négative. Mince, je fais quoi? Valeur absolue?

Non les statisticiens ils mettent tout au carré. Je vais faire pareil ça va en plus m'accentuer les extrêmes ce qui n'est pas une mauvaise chose. Ptet ils ont raison en fait avec leurs trucs au carré.

Je calcule ensuite la moyenne de toutes ces "distances relatives" (aucune idée de comment appeler ce facteur) qui devrait idéalement être la plus faible possible.

Quand c'est plus petit que 1 c'est vaguement un genre de pseudo-pourcentage d'erreur sur le comptage. Si un vrai mathématicien me lit iel vient sûrement de vomir un peu dans sa bouche mais bon, je suis juste un expert en CSS moi à la base.

Par exemple pour le modèle de régression linéaire qui ne passe pas par l'origine, la moyenne de ces "distances" est de 0,1558 avec ces données que personne n'a demandé:

Nbre mots	Nbre mots prédit	Distance	Distance rel.	Longueur
7	-3	-10	1.4286	188
75	151	76	1.0133	1433
35	10	-25	0.7143	294
2312	3393	1081	0.4676	27594
90	48	-42	0.4667	598
88	48	-40	0.4545	600
477	693	216	0.4528	5800
923	1316	393	0.4258	10833
51	31	-20	0.3922	459
135	85	-50	0.3704	898
11	7	-4	0.3636	270
787	1062	275	0.3494	8782
1251	1685	434	0.3469	13811
127	83	-44	0.3465	878
1077	1441	364	0.3380	11841
225	156	-69	0.3067	1467
108	75	-33	0.3056	813
2252	2907	655	0.2909	23668
299	222	-77	0.2575	1999
1303	1633	330	0.2533	13390
576	431	-145	0.2517	3688
486	365	-121	0.2490	3158
424	322	-102	0.2406	2809
671	513	-158	0.2355	4352
34	42	8	0.2353	552
861	667	-194	0.2253	5590
493	383	-110	0.2231	3306
602	471	-131	0.2176	4014
6192	7529	1337	0.2159	60970
3722	4515	793	0.2131	36650
789	956	167	0.2117	7930
484	586	102	0.2107	4939
328	259	-69	0.2104	2302
1255	992	-263	0.2096	8213
585	468	-117	0.2000	3989
20	16	-4	0.2000	337
1061	857	-204	0.1923	7128
1061	858	-203	0.1913	7132
538	438	-100	0.1859	3748
247	202	-45	0.1822	1839
207	170	-37	0.1787	1582
2625	3080	455	0.1733	25064
971	1137	166	0.1710	9388
2339	2725	386	0.1650	22204
807	674	-133	0.1648	5648
5810	6763	953	0.1640	54790
485	564	79	0.1629	4762
185	155	-30	0.1622	1466
485	408	-77	0.1588	3500
5462	4603	-859	0.1573	37355
499	421	-78	0.1563	3608
499	421	-78	0.1563	3608
9459	7999	-1460	0.1544	64762
844	716	-128	0.1517	5986
1610	1369	-241	0.1497	11261
710	604	-106	0.1493	5089
432	496	64	0.1481	4212
776	664	-112	0.1443	5570
398	346	-52	0.1307	3007
261	294	33	0.1264	2581
1140	996	-144	0.1263	8251
1352	1182	-170	0.1257	9751
13964	12237	-1727	0.1237	98961
481	422	-59	0.1227	3618
1394	1227	-167	0.1198	10109
1279	1431	152	0.1188	11763
1579	1764	185	0.1172	14444
1968	1742	-226	0.1148	14270
333	296	-37	0.1111	2604
169	187	18	0.1065	1717
929	1027	98	0.1055	8498
96	106	10	0.1042	1068
1251	1125	-126	0.1007	9289
766	694	-72	0.0940	5815
922	1008	86	0.0933	8348
1770	1609	-161	0.0910	13198
998	912	-86	0.0862	7570
1698	1556	-142	0.0836	12765
1338	1228	-110	0.0822	10124
754	694	-60	0.0796	5815
291	268	-23	0.0790	2378
447	482	35	0.0783	4103
862	928	66	0.0766	7700
2688	2887	199	0.0740	23507
5916	6338	422	0.0713	51359
1240	1152	-88	0.0710	9508
1020	948	-72	0.0706	7865
850	790	-60	0.0706	6585
2267	2109	-158	0.0697	17232
543	506	-37	0.0681	4294
7762	8224	462	0.0595	66575
1135	1068	-67	0.0590	8832
196	185	-11	0.0561	1707
3355	3177	-178	0.0531	25852
2006	2112	106	0.0528	17253
1613	1528	-85	0.0527	12540
5792	5488	-304	0.0525	44498
725	763	38	0.0524	6365
1027	975	-52	0.0506	8080
2290	2403	113	0.0493	19607
1708	1792	84	0.0492	14675
587	559	-28	0.0477	4720
1238	1295	57	0.0460	10660
1494	1431	-63	0.0422	11762
9491	9111	-380	0.0400	73737
3475	3337	-138	0.0397	27144
20286	21085	799	0.0394	170366
4270	4108	-162	0.0379	33360
4318	4454	136	0.0315	36158
19109	18516	-593	0.0310	149634
1666	1717	51	0.0306	14065
10447	10758	311	0.0298	87027
1310	1273	-37	0.0282	10482
370	360	-10	0.0270	3113
446	458	12	0.0269	3906
4412	4317	-95	0.0215	35045
1426	1397	-29	0.0203	11481
1580	1548	-32	0.0203	12704
2543	2494	-49	0.0193	20334
737	724	-13	0.0176	6054
1627	1604	-23	0.0141	13152
8816	8728	-88	0.0100	70643
2587	2610	23	0.0089	21270
10217	10129	-88	0.0086	81951
258	256	-2	0.0078	2281
1471	1481	10	0.0068	12159
7354	7402	48	0.0065	59946
2030	2018	-12	0.0059	16499
3707	3724	17	0.0046	30266
9369	9407	38	0.0041	76120
514	512	-2	0.0039	4344
2883	2892	9	0.0031	23551
1739	1744	5	0.0029	14284
1561	1563	2	0.0013	12824

Les résultats sont classés avec les pires cas en premier. On constate un nombre non négligeable de prédictions très correctes.

Modèle "multifacteur"

L'idée de ce plan m'est venue parce qu'on dirait que les "moyennes locales" de ratio sont différentes selon qu'on soit en deçà de 2000 de longueur ou au delà de 10000. En gardant à l'esprit que tout ça est évidemment plutôt arbitraire.

Je peux donner plusieurs "facteurs" accompagnés d'une plage de longueur à mon programme, en plus du facteur par défaut qui est utilisés quand aucune des plages de longueur ne s'applique.

Ceci signifie accessoirement que j'ai du ajouter encore plus de logique à mon programme pour interpréter des paramètres multiples et séparés par des virgules sur la ligne de commande.

C'est pas tout perdu parce que je suis un peu à la recherche d'un bon écosystème pour créer des utilitaires en ligne de commande sans trop se prendre la tête.

La librairie Clap pour Rust est super. Evidemment ici on est en Go.

Je me suis décidé à essayer le module flag faisant partie de la librairie standard Go (rien à installer du coup) et ça fait assez bien le taf.

Je pense qu'il y avait même moyen d'accompagner véritablement un utilitaire avec plusieurs "modes" mais je ne l'aurai compris que par après et, contrairement aux apparences, je n'ai pas une autre trentaine d'heures à consacrer à cette affaire.

Pour trouver les différents "facteurs" j'ai dû ajouter un moyen de donner une plage de longueurs min et max au premier mode du programme (j'ai oublié comment je l'ai appelé ici ce mode):

go run cmd/wordstats/main.go -mode plot -ignore-ids 79 -start-length 0 -end-length 1500

Une fois qu'on a collecté quelques "facteurs" pseudo-arbitraires à l'arrache on peut les entrer dans le mode vérification:

go run cmd/wordstats/main.go -mode verify -ignore-ids 79 -default-factor 0.120256 -factor 0.112252,0,2500 -factor 0.125722,2500,15000

On s'amuse nettement plus que dans une feuille de calcul non? Non? Bon d'accord.

En pratique ce modèle demande pas mal d'effort et est très vulnérable au biais-de-données-courantes qui est un truc que j'ai inventé pour exprimer l'idée que je vais essayer de tailler les facteurs pour répondre précisément au jeu d'articles du moment mais que trois nouveaux articles plus tard ce sera de nouveau moins bien que la régression linéaire. même moi j'ai rien suivi de cette phrase et je vais pas la relire.

Pour la même raison, je pense que c'est inutile d'essayer d'optimiser cette technique avec un algorithme (non pas que j'avais l'intention de le faire hein 💩).

La simple réalité que j'arrive pas à faire mieux que la régression linéaire en choisissant jusque 3 catégories (vraiment pas envie de faire plus lol) prouve que ce modèle sent un peu le pâté.

Ceci dit il est pas totalement naze. En fait, si et seulement si on retire au moins l'article-qui-n'a-qu'un-seul-mot du jeu de données, il est équivalent à la régression linéaire avec déviation de l'origine.

Résultats et choix d'un modèle

Sur demande générale de tout le monde, voici les résulats de quelques uns de mes "modèles".

Et oui avant que vous ne posiez la question, ces graphiques d'une rare beauté ont été sortis par une feuille de calcul.

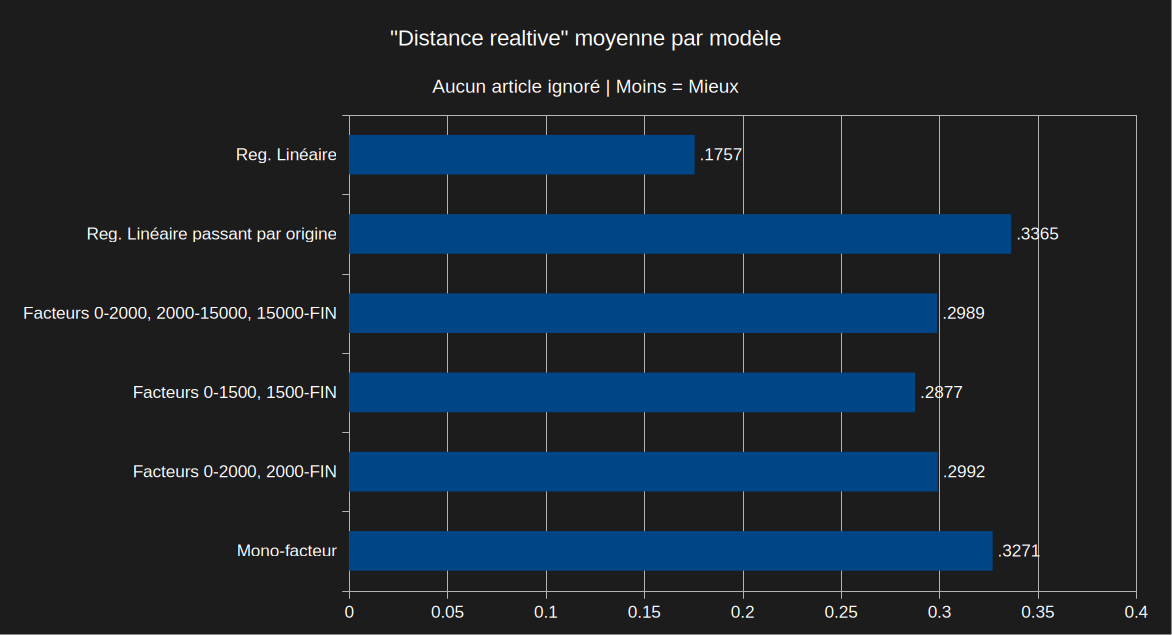
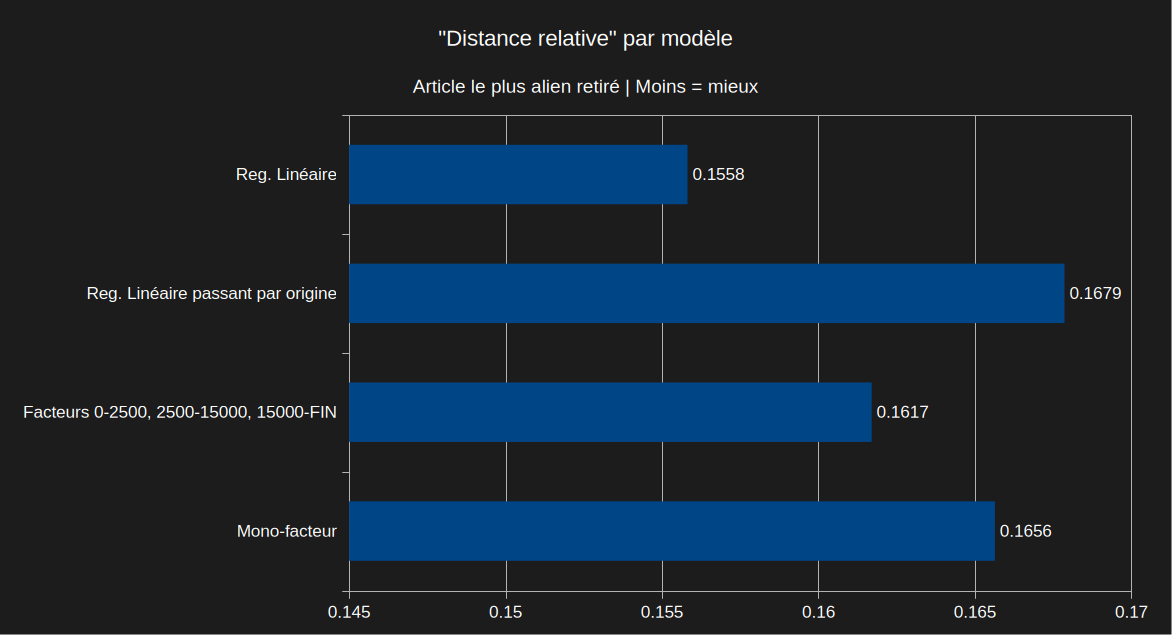
Commençons par les prédictions avec tous les articles présents.

La régression linéaire dépasse de loin les autres options qui trainent toutes à peu près dans la même médiocrité.

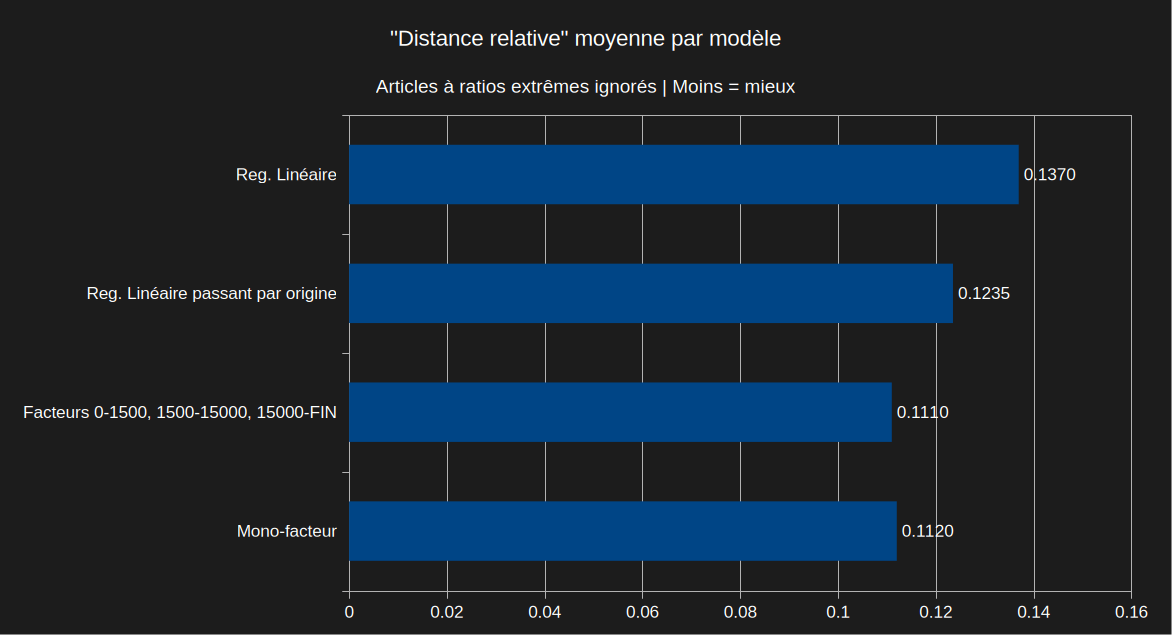
Passons ensuite aux prédictions avec l'article au ratio nombre de mots sur longueur le plus improbable retiré des données. Notez que je re-calcule les paramètres chaque fois, ce ne sont pas les mêmes paramètres testés sur un jeu de données différent.

La régression linéaire est toujours en tête. Le "mono-facteur" (utilise la moyenne comme coefficient de régression linéaire passant par l'origine) est très correct aussi.

J'avais envie de pousser le vice plus loin et retirer plusieurs articles avec des ratios un peu extrêmes du calcul, et dans ce cas là le "mono-facteur" l'emporte mais c'est normal puisque j'ai retiré une bonne partie de ce qui générait de la dispersion par rapport à la moyenne, et le "mono-facteur" c'est précisément la moyenne.

Je suis au courant que le plan "tri-facteur" est devant sauf que j'ai déjà expliqué pourquoi je suis pas fan de ce modèle et il ne l'emporte que d'un micro poil d'orteil.

Ma conclusion extrêmement scientifique et raisonnée va être de choisir la régression linéaire (complète, avec déviation de l'origine) — Ce qui est formidable parce que mon programme en Go est incapable de la calculer.

Ce sera du boulot pour une autre fois, je compte bien mettre à jour la formule quand le nombre d'article augmente. Je compte bien! J'ai pas dit que je le ferai (je ferai pas).

Est-ce que tout ceci avait vraiment un sens?

Faisons peter le max de prétention masturbatoire que je puisse personnellement invoquer depuis que j'ai lu ce fameux bouquin sur les algorithmes dans le but de passer des entretiens d'embauche chez Google.

En vrai j'ai pas tout compris à ce livre et passé la moitié des pages en concluant que j'allais pas poster chez Google.

Il y a cependant un concept très important pour lequel les mathématiciens nous détestent parce qu'on fait semblant d'être des experts en abstractions mathématiques avec de bons gros raccourcis: la notation BIG O.

Pour résumer simplement cette histoire de notation: si on a un jeu de données avec n échantillons sur lesquels on applique un algorithme, cet algorithme va prendre un certain temps qu'on aimerait bien réduire au possible pour sauver la planète (et surtout de l'argent en temps et énergie).

Ce temps est souvent fonction de n lui-même, et souvent de manière linéaire, ce qu'on désigne par O(n) pour avoir l'air intelligent. Normalement quand on l'évoque on explique surtout rien de ce que je viens d'expliquer parce qu'au moins les gens comprennent au mieux c'est pour montrer comment vous êtes l'élite de l'optimisation à induction.

Parcourir chaque lettre d'un texte de n caractères, ça prend de plus en plus de temps au plus il y a de caractères.

Appliquer une vieille formule truc=machin*bidule ça prend toujours le même temps, on appelle ça O(1) et ce sont les meilleurs algorithmes (sauf si le temps pour la mono-itération est de 460 ans).

Les modèles de language qu'on utilise aujourd'hui pour tout faire ont une complexité O(qmlsdkfjqmlskdfjmqlsdkjf). Ce qui est pas top. Oui, en 2025 tout le monde s'en balance d'optimiser quoi que ce soit. Limite au plus ton "algorithme" implique de cartes graphiques et d'actions Nivida au mieux ça attire les investisseurs.

Maintenant que vous avez eu un aperçu de mes compétences étendues en sciences de l'ordinateur, je n'ai pas vraiment de doute que mon calcul de régression linéaire soit plus rapide que de compter les mots (équivaut plus ou moins à compter les espaces) dans une chaîne de caractère.

La question est plutôt de mesurer l'[in]utilité du gain.

Etant donné le temps déjà perdu sur le reste de mes projets persos avec cet "algorithme" (faut le dire vite) de calcul de temps de lecture de blog, je dois me limiter à du TEST à L'ARRACHE.

Je pourrais juste compter les mots comme ceci et considérer l'estimation comme suffisante:

function minutesUsingCounting(content) {
  let count = 0;
  for (let i = 0; i < content.length; i++) {
    if (content[i] === " ") {
      count++;
    }
  }
  return (count + 1) / wordsPerMinute
}

Où wordsPerMinute représente le taux de lecture choisi pour l'humain moyen lecteur de mon blog (risque d'être compliqué à mesurer pour différentes raisons).

Par contre je sais même pas comment on benchmark du JavaScript dans un navigateur.

Je vois que ça parle de console.time("<NAME>") et console.timeEnd("<NAME>") mais ça a l'air de sentir la cave et se limite à la milliseconde de précision.

Si je mesure une seule fois l'opération, c'est beaucoup trop long une milliseconde pour mon ordi portable même sur batterie. Les deux opérations (avec formule ou comptage de mots) prennent 0 ou 1ms d'après le truc alors que j'ai choisi l'article le plus long qui devrait en théorie pénaliser davantage le comptage de mots (vous vous souvenez de la notation BIG O?).

Sur le site MDN j'ai déterré un autre plan: performance.now() — Il est aussi en millisecondes, mais ils disent que ce sont de meilleures millisecondes. Si vous avez mieux faites peter les commentaires s'il vous plait moi j'ai pas le temps.

A vue de nez ça change pas grand chose mais bon. Peut-être que c'est parce que j'utilise Firefox à une époque où il est encore plus abandonné que d'habitude.

Cette fois-ci j'ajoute aussi un décompte en utilisant la méthode split() des strings en JavaScript, ce qui me semble être la pire idée au monde mais Claude me l'a suggéré alors ajoutons-là au cas où.

En gros c'est ça son plan:

function minutesUsingSplit(content) {
  return content.split(' ').length / wordsPerMinute
}

Et ça change pas grand chose, à part qu'on "dirait" que la régression linéaire reste plus souvent à 0ms. Chouette.

Je crois que les gens ils répètent simplément l'opération 1000 ou 10000 fois histoire d'avoir une différence significative.

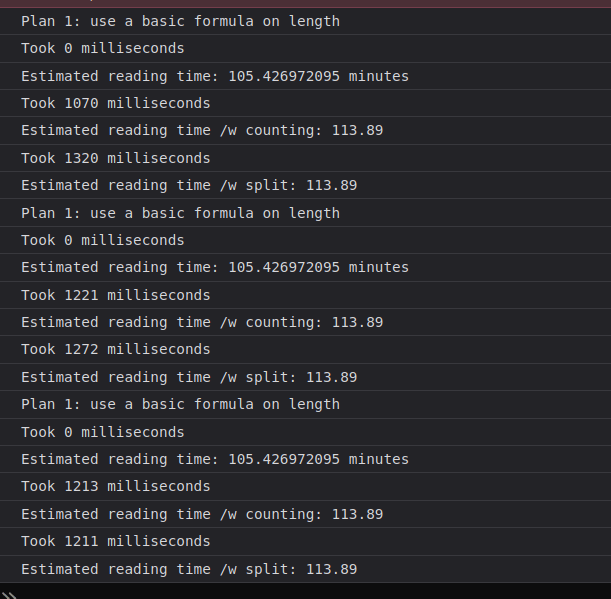
Dans ce cas la différence apparaît tout à coup tel le relief de mes pecs quand je m'étire le matin (si on arrive à lire cette diarrhée de console.log mal étiquettés — désolé mais je refais pas les captures d'écran):

OK donc les autres techniques prennent plus ou moins le même temps, et la formule reste immédiate (POURQUOI je dis ça GENRE çA m'éTONNE????).

Tant qu'on y est à tester des trucs j'en profite pour ajouter la "méthode regex" que j'imagine être la plus lente:

const spaceReg = / /g

function minutesUsingRegex(content) {
  const matches = content.match(spaceReg)
  return matches ? matches.length / wordsPerMinute : 0
}

J'ai mis la regex comme variable globale en me disant que ce serait une optimisation complémentaire si l'interpréteur peut la compiler une seule fois, mais on dirait que l'ajouter dans le corps de la fonction ne change rien en terme de performances.

J'imagine que le runtime JavaScript optimise en compilant à l'avance de toutes façons. Ou un truc du genre?

Toujours est-il qu'avec 1000 itérations, cette technique ne prend en fait pas vraiment plus de temps que les autres:

J'ai aussi juste testé 50 itérations comme ça pour rigoler et on voit clairement que la technique "split" prend plus de temps que les autres avec la technique regex légèrement plus lente que compter les mots.

J'imagine que c'est un peu comme "simuler" un système 50 fois plus lent? Peut-être? Non?

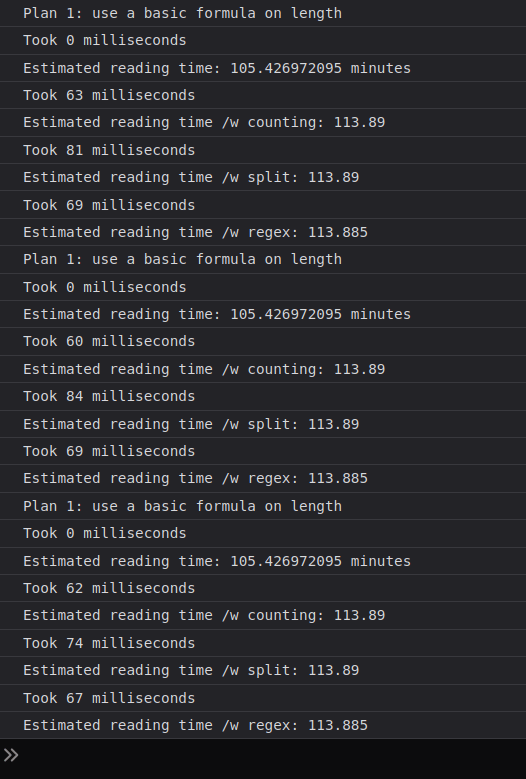
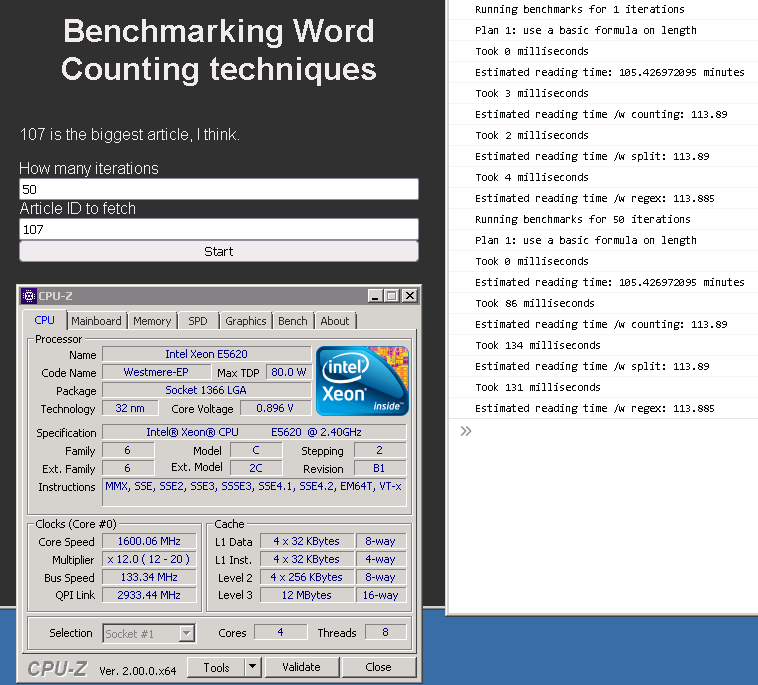
J'ai tenté de déterrer le processeur le plus ancien que j'aie à disposition sans devoir piller une tombe et réinstaller Windows XP (ça se passe toujours dans cet ordre là) qui s'avère être un Westmere (antérieur à la génération "2" d'Intel (SandyBridge)) et même avec une seule itération il y a cette fois-ci une différence (oui j'ai ajouté un machin pour spécifier le nombre d'itérations):

Par contre la formule prend toujours 0ms. Idem avec plus d'itérations sur cette vieille machine. Il semblerait que JavaScript soit capable de multipler deux nombres (à virgule flottante! Attention!) en moins de 1ms.

Quand je lis ce que viens d'écrire j'ai juste "ben ouais... Evidemment, tu croyais quoi??" qui me vient en tête mais c'est trop tard pour retravailler cette section.

Je constate aussi qu'au plus la machine est balaise, au moins il y a de différence entre les mesures (ou du moins, il faut ajouer un gros tas d'itérations pour le voir) et il y a encore d'autres effets bizarres ou la méthode regex se retrouve derrière la méthode "split", pour 10000 itération uniquement si l'ordi est branché sur le secteur. Sinon "split" est plus lente.

On va dire que c'est cool. Même si ça change rien sur mon ordi avec le plus long article du blog (dans la plupart des contextes, 1ms=rien). Je savais dès le début que ce serait comme ça.

J'ai posé le "bench" en ligne si mon code à l'arrache à base de console.log dans un ordre discutable intéresse quelqu'un. Il est configuré pour utiliser la vraie API du blog.

Conclusion

J'aurais estimé le temps de lecture de cet article à 31 minutes. Raisonnable n'est-ce pas?

Voilà la vie peut continuer maintenant.

J'en parle plus haut dans le contexte de l'efficacité algorithmique, mais si on veut la pire efficacité possible au monde pour l'estimation du temps de lecture, les gros LLM sont très forts pour ça.

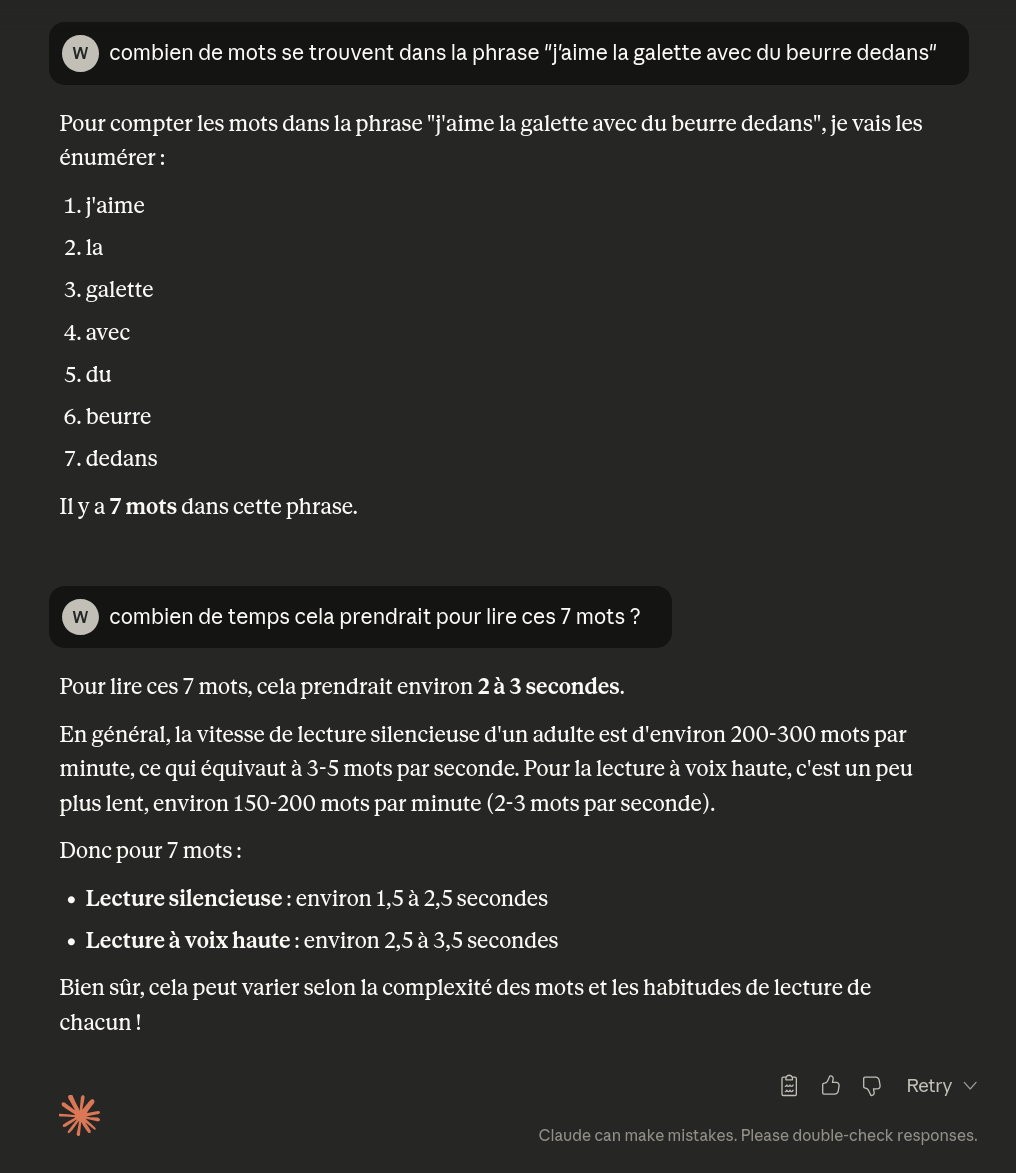
J'ai pas essayé avec un modèle en local. A mon avis il aurait fait le taff aussi. Après tout les modèles de langage découpent ce qu'on leur demande en mots, c'est un peu le principe de base.

Du coup est-ce vraiment étonnant qu'ils soient forts pour compter des mots? Ben non. C'est un peu plus étonnant qu'ils soient capables de maths si on a envie d'être étonné.

De toutes façons, moi, j'ai même pas besoin de compter des mots c'est ça la conclusion wesh.